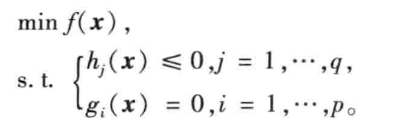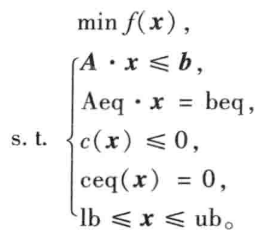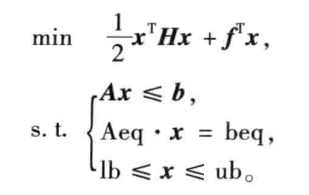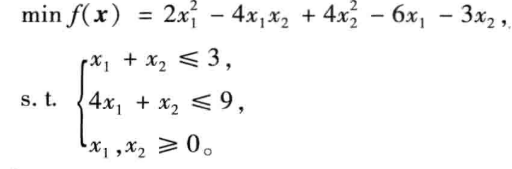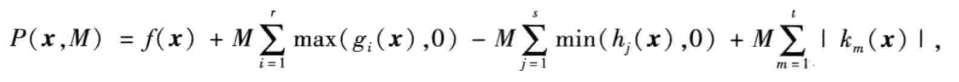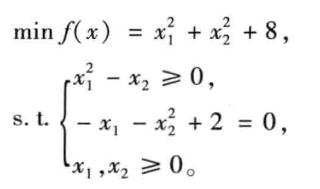线性规划
定义:
- 可行解:满足约束条件的解,使目标函数达到最大的可行解称为最优解。
- 可行域:所有可行解构成的集合。
MATLAB中线性规划的标准形式
其中的为列向量,为价值向量,为资源向量;,为矩阵。 MATLAB的求解线性规划的命令:
1
2
3
| [x,fval]=linprog(f,A,b)
[x,fval]=linprog(f,A,b,Aeq,beq)
[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub)
|
x返回决策向量的取值,fval返回目标函数的最优值,A和b对应线性不等式约束;Aeq和beq对应线性等式约束;lb和ub分别对应决策向量的下界向量和上界向量。 ### 例子


相关应用
可以参考博客:投资的收益与风险的数学建模
整数规划
数学规划中变量限制为整数时,称为整数规划。线性规划模型中,变量限制为整数,则称为整数线性规划。目前流行的求解整数规划的方法,大多只适用于整数线性规划。 整数规划有两大类:
- 变量全限制为整数,纯整数规划
- 变量部分限制为整数,混合整数规划
整数规划特点: 1.原线性规划有最优解,当自变量限制为整数后,其整数规划解出现下述情况:
- 原线性规划最优解全是整数,则整数规划最优 解与线性规划最优解一致。
- 整数规划无可行解 求解方法分类
- 有可行解(当然就存在最优解),但最优解值变差。
2.整数规划最优解不能按照实数最优解简单取整而获得。
求解方法分类: 1.分枝定界法—可求纯或混合整数线性规划。 2.割平面法—可求纯或混合整数线性规划。 3.隐枚举法—求解“0-1”整数规划。
4.匈牙利法—解决指派问题(“0-1”规划特殊情形)。 5.蒙特卡洛法—求解各种类型规划。
0-1整数规划
相互排斥的约束条件
0-1型整数规划是整数规划中的特殊情形,它的变量仅取0或1。这时称为0-1变量,或称二进制变量。仅取值0 或 1 这个条件可由下述约束条件:
,且为整数
所代替,是和一般整数规划的约束条件形式一致的。



固定费用问题

指派问题
拟分配人去做项工作,每人做且仅做一项工作,若分配第人去做第项工作,需花费单位时间,问应如何分配工作才能使工人花费的总时间最少? 要给出一个指派问题的实例,只需给出矩阵,被称为指派问题的系数矩阵。 引入0-1变量:
第人做第项工作第人做第项工作
。
上述指派问题的数学模型:
,,或。
上述指派问题的可行解可以用一个矩阵表示,每行、每列均有且只有一个元素为1,其余元素均为0。(因为一个人只能做一项工作)
蒙特卡洛(随机取样)
蒙特卡洛方法也称为计算机随机模拟方法,它源于世界 著名的赌城—摩纳哥的 Monte Carlo(蒙特卡洛)。它是基于 对大量事件的统计结果来实现一些确定性问题的计算。 蒙特卡洛方法可分为两类:
- 所求解的问题本身具有内在的随机性,借助计算机的 运算能力可以直接模拟这种随机的过程。
- 所求解问题可以转化为某种随机分布的特征数,比如 随机事件出现的概率,或者随机变量的期望值。用于求解复杂的多维积分问题。
蒙特卡洛法必须使用计算机生成相关分布的随机数,Matlab给出了生成各种随机数的命令。
例子1
若想求得图中不规则阴影部分的面积:
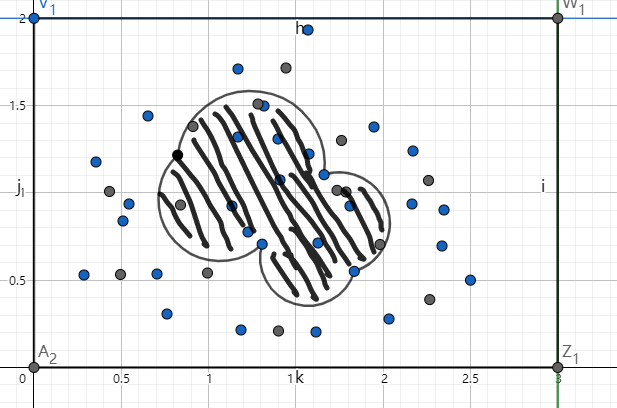
可以在规定的矩形区域内生成随机点,设点在不规则图形内部的数量为,全部的随机点为,矩阵面积为,则不规则阴影面积可以近似为:
例子2
可以参考蒙特卡洛算法的MATLAB实现的例子
非线性规划
非线性规划模型
定义:目标函数或约束条件中包含非线性函数 一般形式:
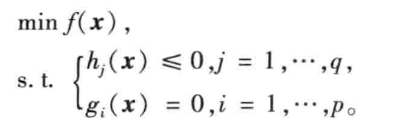
与线性规划区别:线性规划的最优解只能在可行域的边界达到,而非线性规划的最优解可能在可行域上的任意一点。 matlab中非线性规划的数学模型标准型:
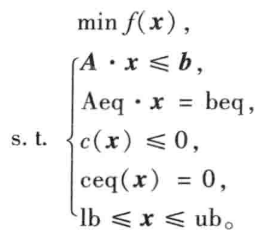
其中部分变量与线下规划相同;为非线性向量函数。
例子
例子求解 
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
function f=fun1(x);
f=sum(x.^2)+8;
function [g,h]=fun2(x);
g=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20];
h=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3];
[x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2')
|
无约束问题
符号解


编写的matlab程序如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| clc, clear
syms x y
f=x^3-y^3+3*x^2+3*y^2-9*x;
df=jacobian(f);
d2f=jacobian(df);
[xx,yy]=solve(df)
xx=double(xx);yy=double(yy);
for i=1:length(xx)
a=subs(d2f,{x,y},{xx(i),yy(i)});
b=eig(a);
f=subs(f,{x,y},{xx(i),yy(i)}); f=double(f);
if all(b>0)
fprintf('(%f,%f)是极小值点,对应的极小值为%f\n',xx(i),yy(i),f);
elseif all(b<0)
fprintf('(%f,%f)是极大值点,对应的极大值为%f\n',xx(i),yy(i),f);
elseif any(b>0) & any(b<0)
fprintf('(%f,%f)不是极值点\n',xx(i),yy(i));
else
fprintf(无法判断(
end
end
|
数值解
例子1
求解多元函数:的极值
1
2
3
4
5
6
7
| clc, clear
f=@(x) x(1)^3-x(2)^3+3*x(1)^2+3*x(2)^2-9*x(1);
g=@(x) -f(x);
[xy1,z1]=fminunc(f, rand(2,1))
[xy2,z2]=fminsearch(g,rand(2,1));
xy2, z2=-z2
|
极小值点:,极小值;极大值点,极大值:
例子2
求函数的极小值
使用函数梯度,编写M函数fun3.m如下:
1
2
3
4
5
6
7
| function[f,g]=fun3(x);
f=100*(x(2)-x(1)^2)^2+(1-x(1))^2;
g=[-400*x(1)*(x(2)-x(1)^2)^2-2*(1-x(1));200*(x(2)-x(1)^2)];
options=optimset('GrandObj','on');
[x,y]=fminunc('fun3',rand(1,2),options)
|
求极值时,利用二阶导数(利用Hessian求解,加入优化参数)
1
2
3
4
5
6
7
8
9
|
function [f,df,d2f]=fun4(x);
f=100*(x(2)-x(1)^2)^2+(1-x(1))^2;
df=[-400*x(1)*(x(2)-x(1)^2)-2*(1-x(1));200*(x(2)-x(1)^2)];
d2f=[-400*x(2)+1200*x(1)^2+2,-400*x(1)
-400*x(1),200];
options = optimset('GradObj','on','Hessian','on');
[x,y]=fminunc('fun4',rand(1,2),options)
|
函数的零点和方程组的解
求多项式 Matlab程序如下:
1
2
3
4
| clc, clear
xishu=[1 -1 2 -3];
x0=roots(xishu)
|
求得多项式的全部零点为-0.1378和1.2757。
使用符号求解如下
1
2
3
| syms x
x0=solve(x^3-x^2+2*x-3)
x0=vpa(x0,5)
|
数值解
1
2
| y=@(x) x^3-x^2+2*x-3;
x=fsolve(y,rand)
|
约束极值问题
二次规划
若某非线性规划的目标函数为自变量的二次函数,约束条件又全是线性的,就称其为二次规划。
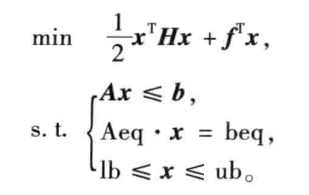
例子:
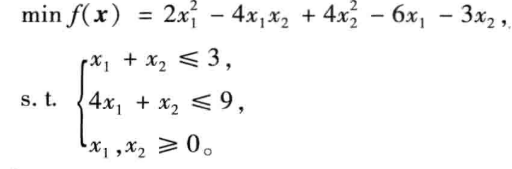
1
2
3
4
5
| h=[4,-4;-4,8];
f=[-6;-3];
a=[1,1;4,1];
b=[3;9];
[x,value]=quadprog(h,f,a,b,[],[],zeros(2,1))
|
求得,,。
罚函数法
序列无约束最小化技术:将非线性规划问题转化为无约束极值问题。 利用问题中的约束函数作出适当的罚函数,由此构造出带参数的增广目标函数,把问题转化为无约束非线性规划问题。
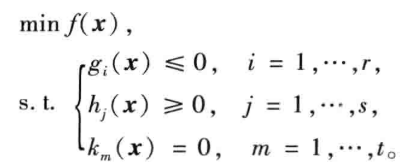
对如上问题,取一个充分大的数,构造函数
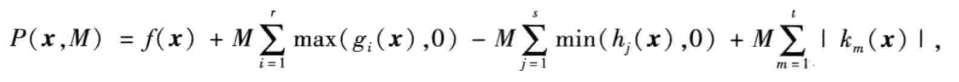
例子 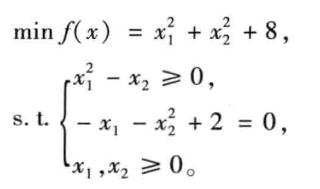
Matlab程序
1
2
3
4
5
6
7
| function g=test3(x);
M=50000;
f=x(1)^2+x(2)^2+8;
g=f-M*min(min(x),0)-M*min(x(1)^2-x(2),0)+M*(-x(1)-x(2)^2+2)^2;
[x,y]=fminsearch('test3',rand(2,1))
|
飞行管理问题
参考博客
···············································································
matlab——整数规划
数学建模—整数规划(笔记)
蒙特卡洛算法的MATLAB实现
第三章:非线性规划
【数学建模学习④】飞行管理问题