数学建模|图与网络模型

发表于 2022-01-11 更新于 2022-05-10 Valine：本文字数： 8.4k 估计阅读时长 ≈ 8 分钟

图论的基本介绍

由于博主专业，在此不再赘述图论的基本知识算法。想了解基础知识，请参考图论（一）基本概念与邻接矩阵

顺带一提：

对于有向图，只要写出邻接矩阵，直接使用Matlab命令：sparse，可以将邻接矩阵转化为稀疏矩阵的表示方式。
对于无向图，由于邻接矩阵是对称的，Matlab中只需要使用邻接矩阵的下三角元素
稀疏矩阵可以使用full命令变成普通矩阵。

最短路径问题

两个顶点之间的最短问题

Dijkstra算法

基本步骤：

首先，定义一个数组 D，D[v] 表示从源点 s 到顶点 v 的边的权值，如果没有边则将 D[v] 置为无穷大。
把图的顶点集合划分为两个集合 S 和 V-S。第一个集合 S 表示距源点最短距离已经确定的顶点集，即一个顶点如果属于集合 S 则说明从源点 s 到该顶点的最短路径已知。其余的顶点放在另一个集合 V-S 中。
每次从尚未确定最短路径长度的集合 V-S 中取出一个最短特殊路径长度最小的顶点 u，将 u 加入集合 S，同时修改数组 D 中由 s 可达的最短路径长度。若加入集合 S 的 u 作为中间顶点时，vi 的最短路特殊路径长度变短，则修改 vi 的距离值（即当D[u] + W[u, vi] < D[vi]时，令D[vi] = D[u] + W[u, vi]）。
重复第 3 步的操作，一旦 S 包含了所有 V 中的顶点，D 中各顶点的距离值就记录了从源点 s 到该顶点的最短路径长度。

Matlab代码及例子

Matlab代码实现

clc,clear all
a=zeros(6);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;               
a(2,3)=15;a(2,4)=20;a(2,6)=25;
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a'                                                  
a(find(a==0))=inf %将a=0的数全部替换为无强大               
pb(1:length(a))=0;pb(1)=1;  %当一个点已经求出到原点的最短距离时，其下标i对应的pb(i)赋1
index1=1; %存放存入S集合的顺序
index2=ones(1,length(a)); %存放始点到第i点最短通路中第i顶点前一顶点的序号
d(1:length(a))=inf;d(1)=0;  %存放由始点到第i点最短通路的值
temp=1;  %temp表示c1,算c1到其它点的最短路。
while sum(pb)<length(a)  %看是否所有的点都标记为P标号
tb=find(pb==0); %找到标号为0的所有点,即找到还没有存入S的点
d(tb)=min(d(tb),d(temp)+a(temp,tb));%计算标号为0的点的最短路，或者是从原点直接到这个点，又或者是原点经过r1,间接到达这个点
tmpb=find(d(tb)==min(d(tb)));  %求d[tb]序列最小值的下标
temp=tb(tmpb(1));%可能有多条路径同时到达最小值，却其中一个，temp也从原点变为下一个点
pb(temp)=1;%找到最小路径的表对应的pb(i)=1
index1=[index1,temp];  %存放存入S集合的顺序
temp2=find(d(index1)==d(temp)-a(temp,index1));
index2(temp)=index1(temp2(1)); %记录标号索引
end
d, index1, index2

Java代码实现

public class DijkstraAlgorithm {

    private final static int N = 10000;     // 约定 10000 代表距离无穷大

    public static void main(String[] args) {
        char[] vertexes = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };    // 顶点
        int[][] weight = {   // 图的邻接矩阵
                    /*A*//*B*//*C*//*D*//*E*//*F*//*G*/
                /*A*/{0,   5,   7,   N,   N,   N,   2},
                /*B*/{5,   0,   N,   9,   N,   N,   3},
                /*C*/{7,   N,   0,   N,   8,   N,   N},
                /*D*/{N,   9,   N,   0,   N,   4,   N},
                /*E*/{N,   N,   8,   N,   0,   5,   4},
                /*F*/{N,   N,   N,   4,   5,   0,   6},
                /*G*/{2,   3,   N,   N,   4,   6,   0}
        };

        int source = 6; // 源点下标
        int[] dis = dijkstra(source, vertexes, weight); // 使用迪杰斯特拉查找最短路径

        // 输出最短路径长度
        for (int i=0; i<dis.length; i++){
            System.out.println(vertexes[source] + "->" + vertexes[i] + " = " + dis[i]);
        }
    }

    /**
     * 迪杰斯特拉算法求解最短路径问题
     * @param source    源点下标
     * @param vertexes  顶点集合
     * @param weight    邻接矩阵
     * @return int[]    源点到各顶点最短路径距离
     */
    public static int[] dijkstra(int source, char[] vertexes, int[][] weight){
        int[] dis;     // 记录源点到各顶点的最短路径长度,如 dis[2] 表示源点到下标为 2 的顶点的最短路径长度
        ArrayList<Character> S = new ArrayList<>(); // 存储已经求出到源点最短路径的顶点，即算法步骤中的 S 集合。

        /* 初始化源点 */
        dis = weight[source];
        S.add(vertexes[source]);

        /* 当 S 集合元素个数等于顶点个数时，说明最短路径查找完毕 */
        while(S.size() != vertexes.length){
            int min = N;
            int index = -1; // 记录已经求出最短路径的顶点下标

            /* 从 V-S 的集合中找距离源点最近的顶点 */
            for (int j=0; j<weight.length; j++){
                if (!S.contains(vertexes[j]) && dis[j] < min){
                    min = weight[source][j];
                    index = j;
                }
            }
            dis[index] = min;   // 更新源点到该顶点的最短路径长度
            S.add(vertexes[index]); // 将顶点加入到 S 集合中，即表明该顶点已经求出到源点的最小路径

            /* 更新源点经过下标为 index 的顶点到其它各顶点的最短路径 */
            for (int m=0; m<weight.length; m++){
                if (!S.contains(vertexes[m]) && dis[index] + weight[index][m] < dis[m]){
                    dis[m] = dis[index] + weight[index][m];
                }
            }
        }
        return dis;
    }
}

每个顶点之间的最短路径

迭代使用n-1次Dijkstra算法

Floyd算法

Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）。 从任意节点i到任意节点j的最短路径不外乎两种可能：

一是直接从i到j，
二是从i经过若干个节点k到j。

所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立。如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

c语言实现

#include <iostream>
#include <cstring>
#include <stack>
#include <queue>
using namespace std;

const int MAX = 65535;

class Graph{
 private:
  int** G;     // 邻接矩阵
  int** dist;     // 距离数组 
  int** path;     // 路径数组 
  int Nv;      // 顶点数
 public:
  //构造函数
  Graph(int nv, int ne){
   this->Nv = nv;
   G = new int*[nv+1];
   dist = new int*[nv+1];
   path = new int*[nv+1]; 
   for(int i = 0 ; i < nv+1 ; i++){
    G[i] = new int[nv+1];
    dist[i] = new int[nv+1];
    path[i] = new int[nv+1];
    memset(path[i],-1,sizeof(path[0][0])*(nv+1));
    for(int j = 0 ; j < nv+1 ; j++){
     this->G[i][j] = this->dist[i][j] = MAX;
    } 
    this->G[i][i] = this->dist[i][i] = 0; 
   }
   cout<<"请输入边与权重:"<<endl;
   for( i = 0 ; i < ne ; i++){
    int v1,v2,weight;
    cin>>v1>>v2>>weight;
    this->G[v1][v2] = this->G[v2][v1] = weight;
    this->dist[v1][v2] = this->dist[v2][v1] = weight;
   } 
  }
  
  //Floyd算法(多源最短路径算法) 
  bool Floyd(){
   for(int k = 1 ; k < this->Nv+1 ; k++){ //k代表中间顶点 
    for(int i = 1  ; i < this->Nv+1 ; i++){//i代表起始顶点 
     for(int j = 1 ; j < this->Nv+1 ; j++){//j代表终点 
      if(this->dist[i][k] + this->dist[k][j] < this->dist[i][j]){
       this->dist[i][j] = this->dist[i][k] + this->dist[k][j];
       if(i == j && this->dist[i][j] < 0){//发现了负值圈 
        return false;
       }
       this->path[i][j] = k;
      }     
     }
    }
   }
   return true; 
  }
  
  // 分治法寻找start到end最短路径的中间结点 
  void Find(queue<int> &q ,int start,int end){
   int mid = this->path[start][end];
   if(mid == -1){
    return;
   }
   Find(q,start,mid);
   q.push(mid);
   Find(q,mid,end);
  }

  //打印start顶点到end顶点的路径 
  void Print_Path(int start,int end){
   queue<int> queue;
   queue.push(start);
   this->Find(queue,start,end); 
   queue.push(end);
   cout<<queue.front();
   queue.pop();
   while(!queue.empty()){
    cout<<"->"<<queue.front();
    queue.pop();
   }
   cout<<endl;
  }
  
  void Print_Floyd(){
   int i,j,k;
   for( i = 1 ; i < this->Nv+1 ; i++){
    for(int j = 1 ; j < this->Nv+1 ; j++){
     cout<<this->path[i][j]<<" ";
    }
    cout<<endl;
   } 
   cout<<" length  path"<<endl; 
   for(i = 1 ; i < this->Nv+1 ; i++){
    for(j = i+1 ; j < this->Nv+1 ; j++){
     cout<<i<<"->"<<j<<" ";
     cout<<this->dist[i][j]<<"  ";  
     this->Print_Path(i,j);
    }
    cout<<endl;
   }
  }
};

int main()
{
 cout<<"请输入顶点数与边长数:"<<endl;
 int nv,ne;
 cin>>nv>>ne; 
 Graph graph(nv,ne);
 if(graph.Floyd()){
  cout<<"各个顶点的最短路径为："<<endl; 
  graph.Print_Floyd();
 }
 
 return 0;
 }

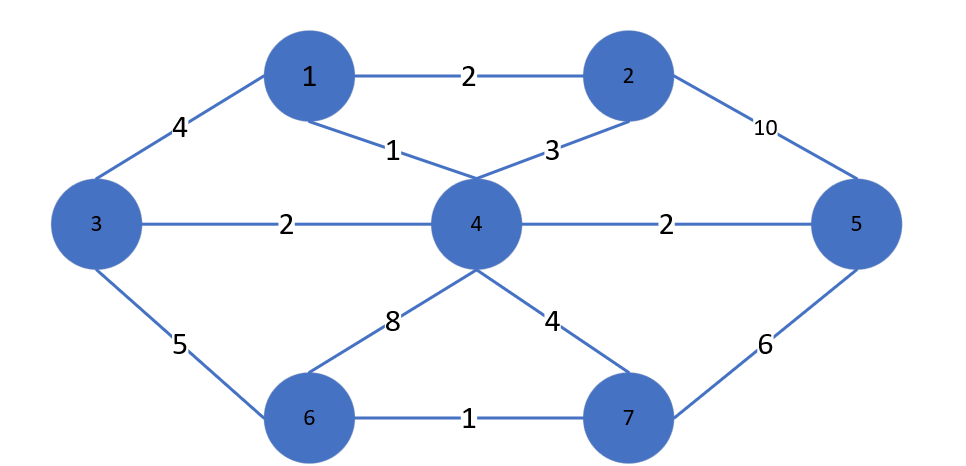
运行结果：

最小生成树

连通的无圈图叫作树，度为1的叫作叶子结点。

应用问题例子：欲修筑连接个城市的铁路，已知城与城之间的铁路造价为,设计一个路线图，使得总造价最低。

Prim算法（以点为主，每次选择下一个中最小权重）

基本思想

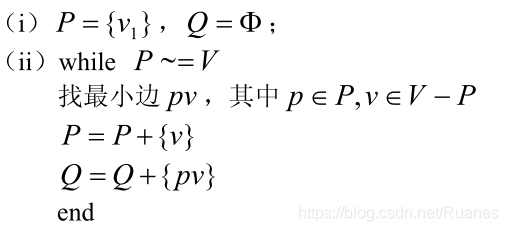
例子：

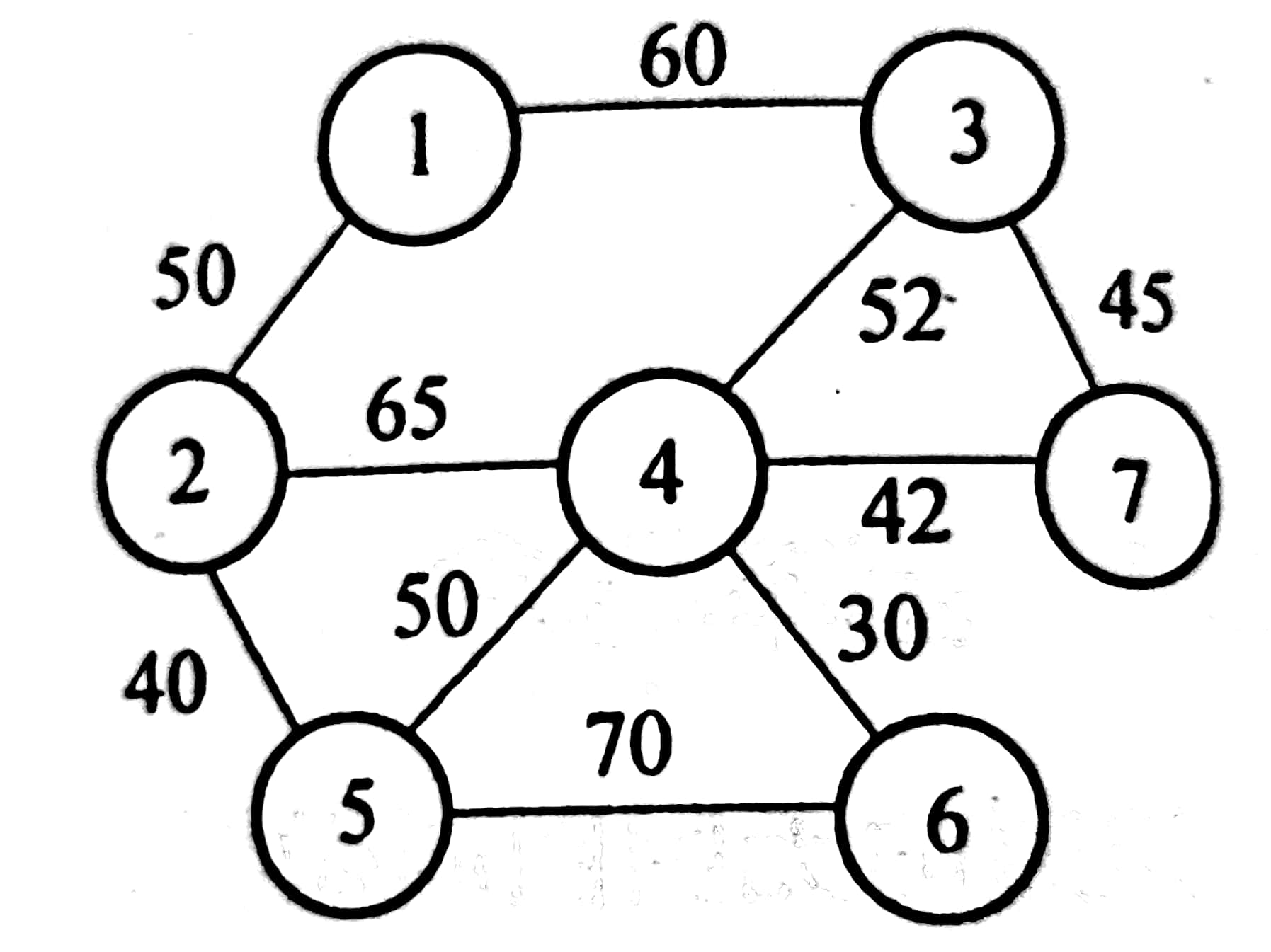
Matlab实现：

clc;clear;
a=zeros(7);
a(1,2)=50;a(1,3)=60;
a(2,4)=65;a(2,5)=40;
a(3,4)=52;a(3,7)=45;
a(4,5)=50;a(4,6)=30;a(4,7)=42;
a(5,6)=70;
a=a+a';a(find(a==0))=inf;
result=[];
p=1;      %起点为1
tb=2:length(a);
while length(result)~=length(a)-1
    temp=a(p,tb);temp=temp(:);
    d=min(temp);
    [jb,kb]=find(a(p,tb)==d);
    j=p(jb(1));k=tb(kb(1));
    result=[result,[j;k;d]];p=[p,k];tb(find(tb==k))=[];
end
result

Kruskal算法(以边为主，每次选最小)

基本思想

将图的n个顶点看作n个分离的部分树，每个树具有一个顶点，算法的每一步就是选择连接两个分离树的具有最小权值的边，将两个树合二为一，直到只有一个树为止（进行n-1步）得到最小生成树。

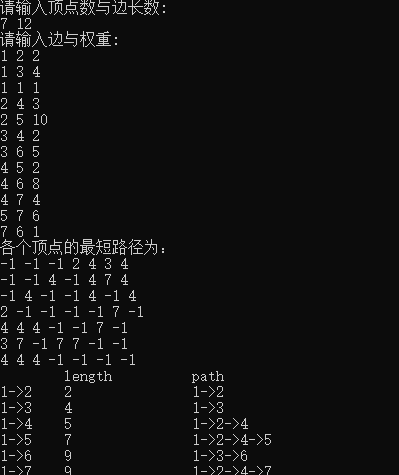
例子：

我们使用边权矩阵进行存储数据，边权矩阵就是按列写入，每列由出发顶点、接收顶点和边的权值组成，如下所示：

%边权矩阵，每一列都表示一条边，从上到下分别为两个顶点以及它们边的权值
b = [1 1 1 2 2 3 3 4;
     2 4 5 3 5 4 5 5;
     8 1 5 6 7 9 10 3];
%sortrows函数对某一列进行比较排序，所以我们先转置b矩阵，然后对第三列也就是权值进行排序
[B,i]=sortrows(b',3);
%再将其转置回来
B=B';
%m为边的条数，n为点的个数
m=size(b,2);n=5;
%t数组用来标记选中的边，k用来计数，T矩阵用来存储选中的边，c计算最小生成树的总长度
t=1:n;k=0;T=[];c=0;

for i=1:m
    if t(B(1,i))~=t(B(2,i))
        k=k+1;T(k,1:2)=B(1:2,i),c=c+B(3,i);
        tmin=min(t(B(1,i)),t(B(2,i)));
        tmax=max(t(B(1,i)),t(B(2,i)));
        for j=1:n
            if t(j)==tmax
                t(j)=tmin;
            end
        end
    end
    if k==n-1
        break;
    end
end
T,c,

网络最大流

何为最大流问题？

参考博客网络流——最大流（全）

Matlab实现

最大流问题(maximum flow problem)，一种组合最优化问题，就是要讨论如何充分利用装置的能力，使得运输的流量最大，以取得最好的效果。管道网络中每条边的最大通过能力（容量）是有限的，实际流量不超过容量。

在数学建模的过程中时长会遇到这种问题，存在专门的算法去解决这一问题，但其实现较为复杂。

MATLAB提供了解决这一问题所使用的函数，即maxflow函数。

语法:

mf = maxflow(G,s,t)
mf = maxflow(G,s,t,algorithm)
[mf,GF] = maxflow(___)
[mf,GF,cs,ct] = maxflow(___)

符号说明：

mf = maxflow(G,s,t) 返回节点 s 和 t 之间的最大流。如果图 G 未加权（即 G.Edges 不包含变量 Weight），则 maxflow 将所有图边的权重视为 1。
mf = maxflow(G,s,t,algorithm) 指定要使用的最大流算法。此语法仅在 G 为有向图时可用。
[mf,GF] = maxflow(___) 还使用上述语法中的任何输入参数返回有向图对象 GF。GF 仅使用 G 中具有非零流值的边构造。
[mf,GF,cs,ct] = maxflow(___) 还返回源和目标节点 ID cs 和 ct，表示与最大流相关联的最小割。

创建并绘制一个加权图。加权边表示流量。

s = [1 1 2 2 3 4 4 4 5 5];
t = [2 3 3 4 5 3 5 6 4 6];
weights = [0.77 0.44 0.67 0.75 0.89 0.90 2 0.76 1 1];
G = digraph(s,t,weights);
plot(G,'EdgeLabel',G.Edges.Weight,'Layout','layered');

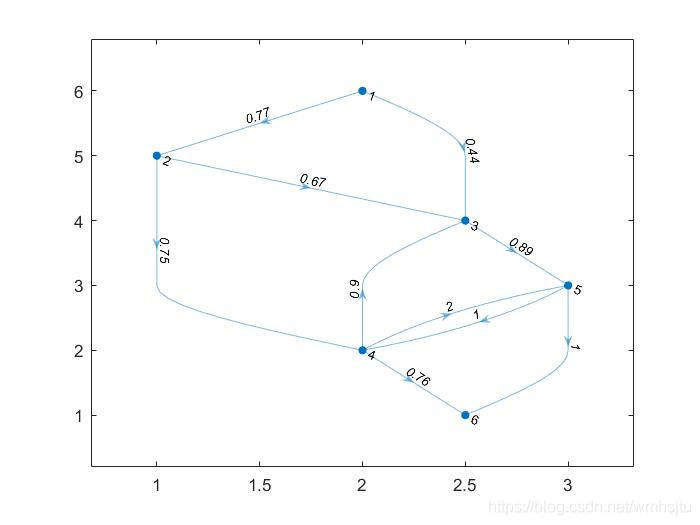
确定节点1到6的最大流:

1	mf = maxflow(G,1,6)

结果：


mf =

    1.2100

参考博客图的最大流问题（含matlab函数使用方法）

图论的基本介绍

最短路径问题

两个顶点之间的最短问题

Dijkstra算法

Matlab代码及例子

Java代码实现

每个顶点之间的最短路径

迭代使用n-1次Dijkstra算法

Floyd算法

c语言实现

最小生成树

Prim算法（以点为主，每次选择下一个中最小权重）

基本思想

Kruskal算法(以边为主，每次选最小)

基本思想

网络最大流

何为最大流问题？

Matlab实现

Matlab图论工具箱