数学建模|回归分析

发表于 2022-01-12 更新于 2022-03-18 Valine：本文字数： 2.9k 估计阅读时长 ≈ 3 分钟

什么是回归分析

人们关心的因变量受自变量的关联性(非因果性)的影响，并且存在众多随机因素，难以用机理分析方法找出它们之间的关系；需要建立这些变量的数学模型，使得能够根据自变量的数值预测因变量的大小，或者解释因变量的变化。

换句话说：回归分析是一种类相关性分析，就是通过分析已知数据和其造成的影响，来预测未知数据造成的影响。

一般来说，回归分析的主要步骤：

收集一组包含因变量和自变量的数据选定因变量与自变量之间的模型，利用数据按照最小二乘准则计算模型中的系数；
利用统计分析方法对不同的模型进行比较，找出与数据拟合得最好的模型；
判断得到的模型是否适合于这组数据, 诊断有无不适合回归模型的异常数据；
利用模型对因变量作出预测或解释。

线性回归

一元线性回归

模型为：

其中：为自变量，,为回归系数，是随机变量(影响的随机因素的总和)。由于是非随机的，可以视作某个常数，故也可以理解为相当于正态总体的参数估计问题。

模型假设

独立：对于不同的相互独立
线性：的期望是的线性函数
齐次：对于不同的的方差是常数
正态：对于给定的服从正态分布

是相互独立的、期望为、方差为，正态分布的随机变量即：,称为随机误差。

回归系数的最小二乘估计

将数据带入，则对随后对求偏导，得出：

误差方差估计

残差：

则的无偏估计：

的自由度=数据容量-模型中含有的参数个数
剩余方差(样本方差)，剩余标准差（样本标准差）

回归系数的区间估计和假设检验

模型的有效性检验

利用一元线性回归模型进行预测

Matlab实现

1 2	b=regress(y,X) [b,bint,r,rint,s]=regress(y,X,alpha)

输入：

y:因变量（列向量）
X:1与自变量组成的矩阵
alpha：显著性水平（若无值，则设为0.05）

输出： - - bint：的置信区间 - r:残差 - rint:残差的置信区间 - s:决定系数 - 值，分布的分位数大于值的概率，当时，模型有效。

多元线性回归

标准方程

保证可逆只需要保证满秩即可，是因为观测y与变量x是有区别的，不然容易混淆。

误差方差估计

归回系数区间估计和假设检验

模型有效性检测

预测

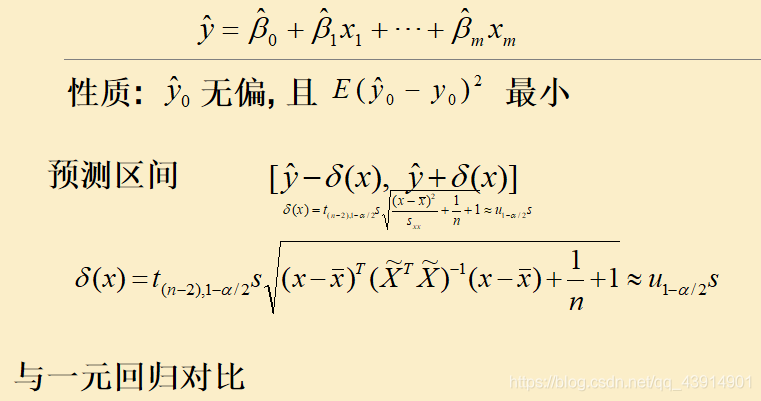
例子

多元线性回归模型：已知某湖八年来湖水中COD浓度实测值(y)与影响因素湖区工业产值(x1)、总人口数(x2)、捕鱼量(x3)、降水量(x4)资料，建立污染物y的水质分析模型。

%输入数据
x1=[1.376, 1.375, 1.387, 1.401, 1.412, 1.428, 1.445, 1.477]
x2=[0.450, 0.475, 0.485, 0.500, 0.535, 0.545, 0.550, 0.575]
x3=[2.170 ,2.554, 2.676, 2.713, 2.823, 3.088, 3.122, 3.262]
x4=[0.8922, 1.1610 ,0.5346, 0.9589, 1.0239, 1.0499, 1.1065, 1.1387]
y=[5.19, 5.30, 5.60,5.82,6.00, 6.06,6.45, 6.95]


 x=[ones(8,1),x1' x2' x3' x4']
[b,bint,r,rint,stats] = regress(y',x)