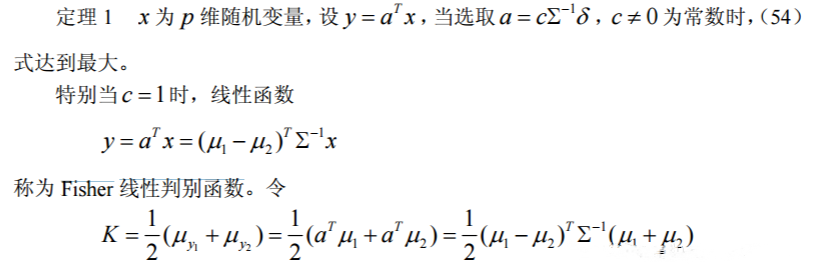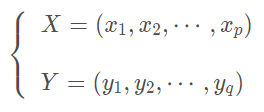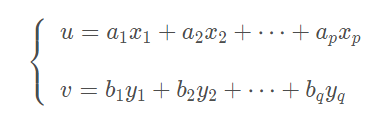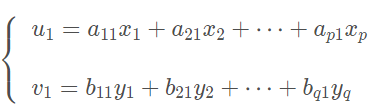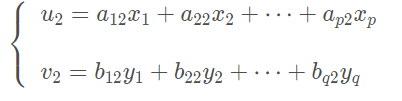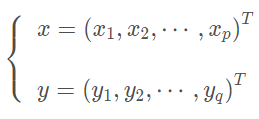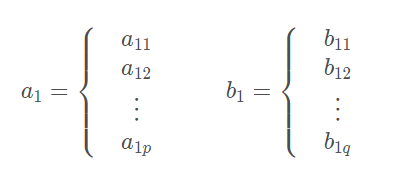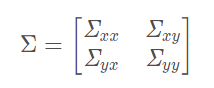判别分析
判别问题用统计的语言来表达,就是已有个总体,它们的分布函数分别为,每个都是维函数。对于给定的样本,要判断它来自哪一个总体。当然,应该要求判别准则在某种意义下是优的,例如错判的概率小或错判的损失小等。我们仅介绍基本的几种判别方法,即距离判别,Bayes判别和Fisher判别。
距离判别
Mahalanobis 距离的概念
通常我们定义的距离是Euclid距离(欧式距离),但是在统计分析里就不适用了。
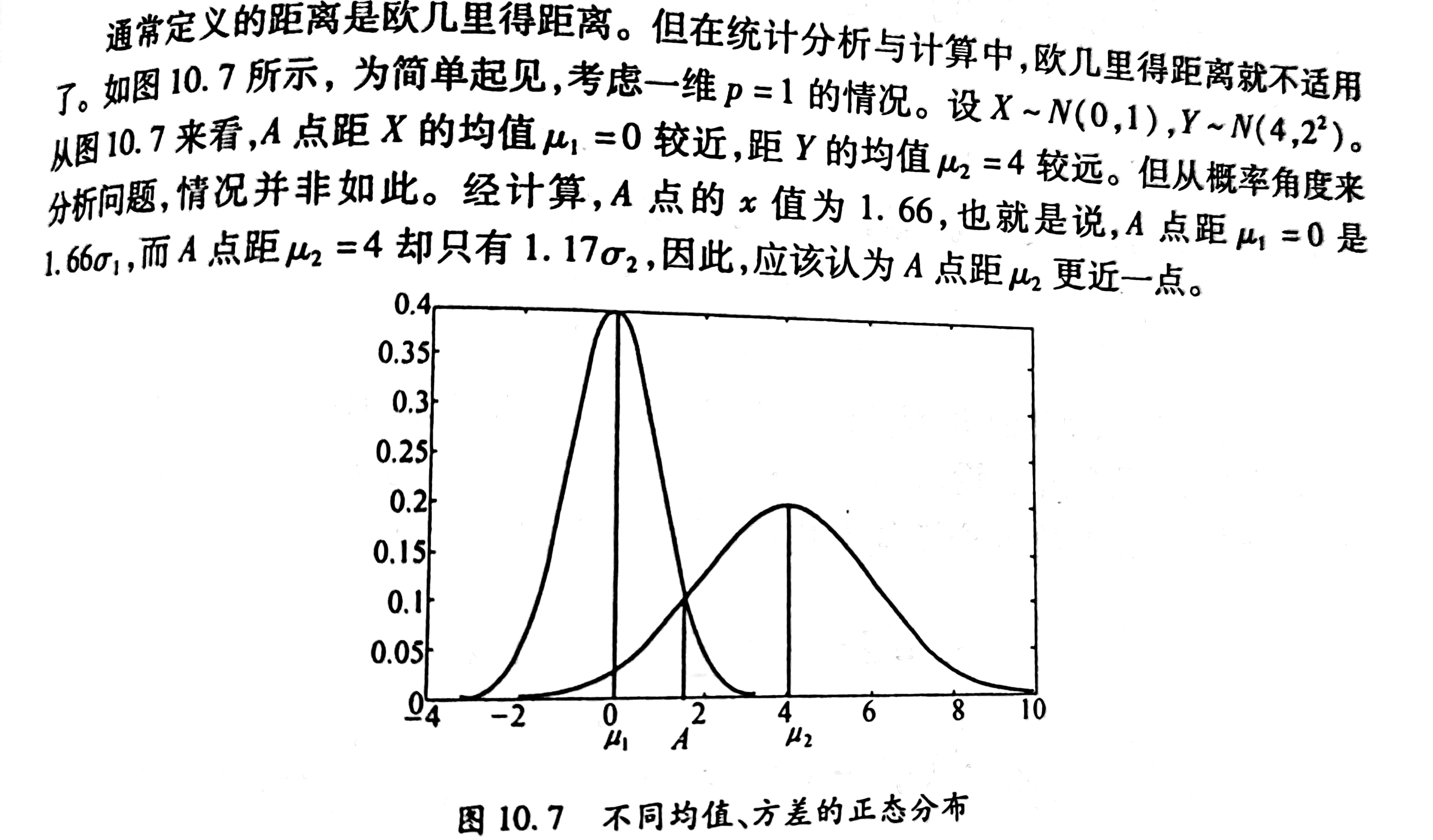
Mahalanobis 距离(马氏距离)的定义

距离判别的判别准则
在这里讨论两个总体的距离判别,分协方差相同和协方差不同两种进行讨论。

两总体距离的判别函数

待测样本的判别函数与判别准则




Fisher判别
Fisher判别的基本思想就是投影,将表面不易分类的数据通过投影到某个方向上使得投影类与类之间得以分离的一种判别方法。


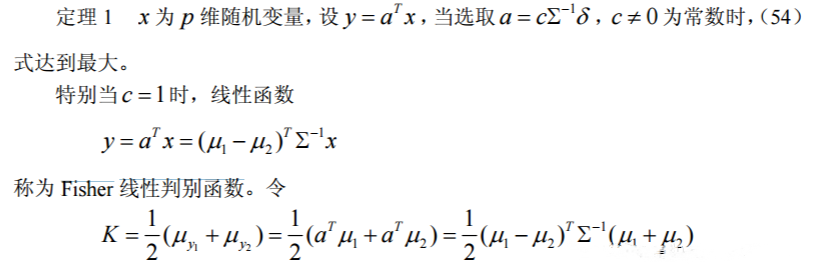

当总体的参数未知时,我们用样本对 及进行估计,注意到这里的 Fisher 判别与距离判别一样,不需要知道总体的分布类型,但两总体的均值向量必须有显著的差 异才行,否则判别无意义。
Bayes判别
Bayes判别和Bayes估计的思想方法是一样的,即假定对研究的对象已经有一定的认识,这种认识常用先验概率来描述,当我们取得一个样本后,就可以用样本来修正已有的先验概率分布,得出后验概率分布,再通过后验概率分布进行各种统计推断。
误判概率与误判损失
设有两个总体和,根据某一个判别规则,将实际上为的个体判为 或者将实际上为的个体判为的概率就是误判概率,一个好的判别规则应该使误判概率最小。除此之外还有一个误判损失问题或者说误判产生的花费(Cost)问题,如把的个体误判到 的损失比的个体误判到严重得多,则人们在作前一种判断时就要特别谨慎。譬如在药品检验中把有毒的样品判为无毒后果比无毒样品判为有毒严重得多,因此一个好的判别规则还必须使误判损失最小。

总体的Bayes判别




建立 Anderson 线性判别函数
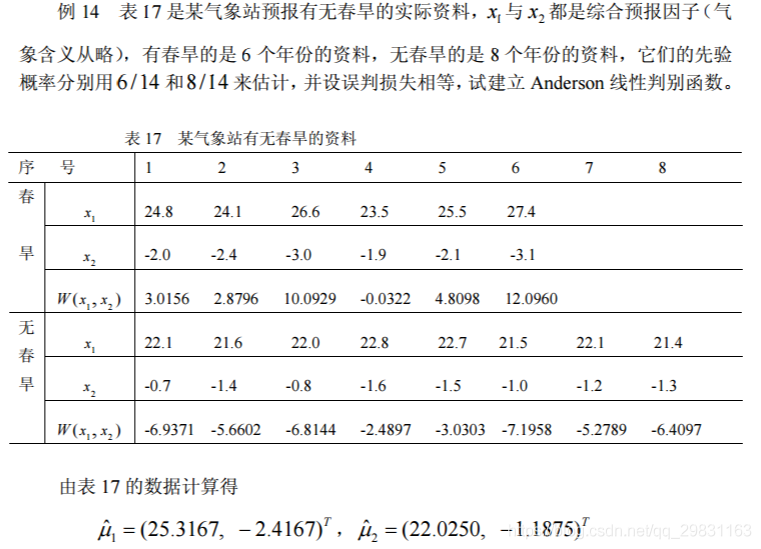

Matlab解决
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| clc,clear
a=[24.8 24.1 26.6 23.5 25.5 27.4
-2.0 -2.4 -3.0 -1.9 -2.1 -3.1]';
b=[22.1 21.6 22.0 22.8 22.7 21.5 22.1 21.4
-0.7 -1.4 -0.8 -1.6 -1.5 -1.0 -1.2 -1.3]';
n1=6;n2=8;
mu1=mean(a);mu2=mean(b);
mu1=mu1',mu2=mu2'
s1=(n1-1)*cov(a),s2=(n2-1)*cov(b)
sigma2=(s1+s2)/(n1+n2-2)
beta=log(8/6)
syms x1 x2
x=[x1;x2];
wx=(x-0.5*(mu1+mu2)).'*inv(sigma2)*(mu1-mu2);
digits(6),wx=vpa(wx)
ahat=subs(wx,{x1,x2},{a(:,1),a(:,2)})
bhat=subs(wx,{x1,x2},{b(:,1),b(:,2)})
|
以下是Σ1 ≠ Σ2 情形下的 MATLAB 程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| clc,clear
p1=6/14;p2=8/14;
a=[24.8 24.1 26.6 23.5 25.5 27.4
-2.0 -2.4 -3.0 -1.9 -2.1 -3.1]';
b=[22.1 21.6 22.0 22.8 22.7 21.5 22.1 21.4
-0.7 -1.4 -0.8 -1.6 -1.5 -1.0 -1.2 -1.3]';
n1=6;n2=8;
mu1=mean(a);mu2=mean(b);
mu1=mu1',mu2=mu2'
cov1=cov(a),cov2=cov(b)
k=log(p2/p1)+0.5*log(det(cov1)/det(cov2))+0.5*(mu1'*inv(cov1)*mu1-mu2'*inv(
cov2)*mu2)
syms x1 x2
x=[x1;x2];
wx=-0.5*x.'*(inv(cov1)-inv(cov2))*x+(mu1'*inv(cov1)-mu2'*inv(cov2))*x;
digits(6),wx=vpa(wx);
wx=simple(wx)
ahat=subs(wx,{x1,x2},{a(:,1),a(:,2)})
bhat=subs(wx,{x1,x2},{b(:,1),b(:,2)})
ahat>=k,bhat<k
|
典型相关分析
通常情况下,为了研究两组变量:
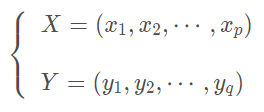
的相关关系,可以用最原始的方法,分别计算两组变量之间的全部相关系数,一共有p × q pqp×q个简单相关系数,这样又烦琐又不能抓住问题的本质。如果能够采用类似于主成分的思想,分别找出两组变量的各自的某个线性组合,讨论线性组合之间的相关关系,则更简捷。
因此,典型相关分析是分析两组变量之间的相关性的一种统计方法,它包含了简单的Pearson相关分析(两组均只含一个变量)和复相关(一组只含一个变量,另一个组含多个变量)这两种特殊情况。
典型相关分析的基本思想和主成分分析的基本思想相似,它将一组变量与另一组变量之间单变量的多重线性相关性研究,转换为少数几对综合变量之间的简单线性相关性的研究,并且这少数几对变量所包含的线性相关性的信息几乎覆盖了原变量组所包含的全部相应信息。
基本思想
假设所研究的两组变量为X组和Y组,其中X组有p个变量
Y组有q个变量
则分别对这两组变量做线性组合后,再计算它们的加权和的简单相关系数,以这个简单相关系数当做这两组变量之间相关性的度量指标,即
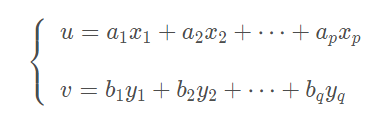
其中,u 和 v 分别是由 x 变量和 y 变量的线性组合产生的综合逐步变量。显然,对任意的一组系数 都可以通过上式求出一对典型变量 u 和 v,在典型相关分析中称之为典型变量。进而可以求出典型变量 u 和 v 的简单相关系数,称之为典型相关系数。 那么,问题来了,怎么进行组合呢?
首先,分别在每组变量中找出第一对线性组合
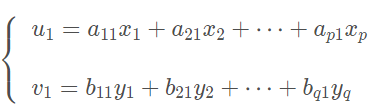
使其具有最大相关性,即使得对应的典型变量和的相关系数为最大。 假设这个最大的
则称为第1典型相关系数,且称具有最大相关系数的这对典型变量和为第1典型变量。
然后再次估计组合系数,在每组变量中找出第二对线性组合,使其分别与本组内的第一线性组合不相关,第二对本身具有次大的相关性
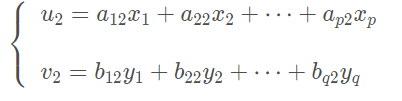
假设这个次大的相关系数是
则称为第2典型相关系数,且称这对典型变量和为第2典型变量。
其中,和与和相互独立,但和相关。如此继续下去,直至进行到 r 步,两组变量的相关性被提取完为止。
可以得到 r 组变量。
从上述分析的过程可以看出,第1对典型变量的第1典型相关系数描述了两个组中变量之间的相关程度,且它提取的有关这两组变量相关性的信息景最多。
第2对典型变量的第2典型相关系数也描述了两个组中变量之间的相关程度,但它提取的有关这两组变量相关性的信总量次多。
依次类推,可以得知,由上述方法得到的一系列典型变量的典型相关系数,所包含的有关原变量组之间相关程度的信息一个比一个少,如果少数几对典型变量就能够解释原数据的主要信息,特别是如果一对典型变量就能够反映出原数据的主要信息,那么,对两个变量组之间相关程度的分析就可以转化为对少数几对或者是一对典型变量的简单相关分析,这就是典型相关分析的主要目的。
典型相关分析的理论以及基本假设
考虑两组变量的向量
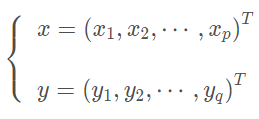
典型相关分析就是寻找 x 组 的线性组合与 y 组的线性组合,使得和之间的简单相关系数为最大,其中
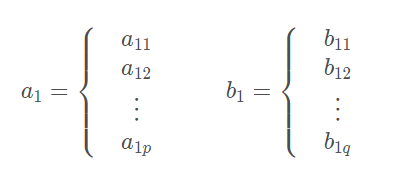
设,x 组与 y 组的协方差阵为
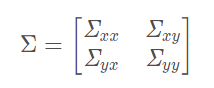


典型相关系数的检验
那么,要选择多少组典型变量呢?
在做两组变量的典型相关分析之前,首先应该检验两组变量是否相关,如果不相关,则讨论两组变量的典型相关就毫无意义.
最多可以选取组,可经由卡方检验决定要选取多少组典型变量。先检验最大的典型根,然后再一个接一个对各个根进行检验,只保留有统计显著性(就是拒绝原假设)的根。
1. 提出假设

2. 当上述原假设被拒绝时,接着做

3. 当上述原假设被拒绝时,接着做
····
4. 依此类推

案例
对应分析
对应分析原理
案例
参考博客
判别分析 ( distinguish analysis)(一):距离判别
典型相关分析(canonical correlation analysis,CCA)