基于热传导的三层玻璃的保暖功效研究

发表于 更新于 Valine： 本文字数： 2.6k 估计阅读时长 ≈ 2 分钟
基于热传导的三层玻璃的保暖功效研究
2022.4.07
王梓涵
摘要

  参考两层玻璃窗保暖效果，本文研究三层玻璃窗的保暖功效。运用初等方法建立模型，建立了方程组使得抽象的热量传导问题具体化、数字化，同时使用Matlab工具完成计算以及绘图，可视化效果更好。

关键词：能量守恒定律 热传导 牛顿冷却定律
一、问题重述
  我国北方许多城镇的一些建筑物都是双层玻璃的，即窗户上装两层玻璃中间留有一定的空隙，如图1与图2。两层厚度为d的玻璃夹着一层厚度为L的空气，据说这样的设计是为了保暖。现在考虑使用三层玻璃，三层厚度为d的玻璃夹着两层厚度为L的空气的情况，并且将三层玻璃窗与同样多材料做成的双增玻璃窗与单层玻璃窗的热量传导进行对比，定量分析三层玻璃窗损失的热量，解释为什么大多数人使用双层玻璃窗而不是三层玻璃窗。
二、模型假设

  该问题主要部分是研究热量传导问题，这与室内外温度、玻璃窗密封状况、玻璃材质、房间保温能力等情况有关，为了便于量化分析与物理规律的适用，现做出如下合理假设：

  • 假设窗户的密封性很好，且玻璃之间的空气没有流动，传导过程没有对流，忽略辐射散热；
  • 玻璃材质均匀，热传导系数是常数；
  • 室内温度与室外温度保持不变，热传导开始即稳定；
  • 室内热量从房门或者其他途径损失忽略不计。
四、符号说明

符号说明要点如下：

符号 解释
\(Q_i\) 热量
\(d\) 玻璃宽度
\(l\) 间隙宽度
\(k\) 热传导系数
五、模型建立

  上述假设成立的情况下，室外和室内的热传导遵循以下牛顿冷却定律：对于厚度为d的均匀介质，若两侧的温差为\(?T\)，则单位时间由温度高的一侧通过单位面积的热量\(Q\)与\(?T\)成正比，与\(d\)成反比，即：

\[ Q=k ?T/d \]

  其中k为热传导系数。   对于三层玻璃，如图所示：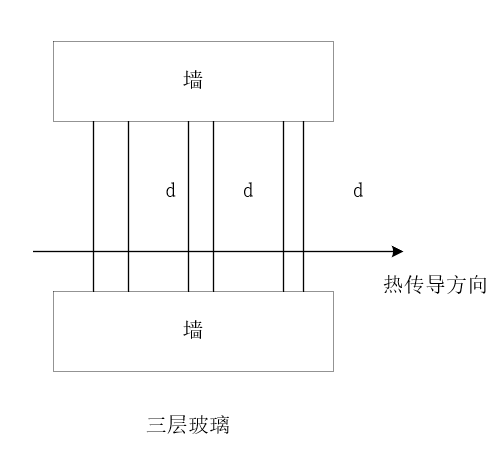

  温度\(T_1、T_2、T_a、T_b、T_a1、T_b1\),玻璃的热传导系数为\(k_1\)，空气的热传导系数为\(k_2\)。根据能量守恒定律，当达到热平衡的时候，由室内传导到窗户上的热量等于窗户内侧传导到外侧的热量，同时也等于窗外侧散失到窗外的热量。 所以三层玻璃的热传导为： \[ T_1-T_a=d/k_1 Q_3 \] \[ T_a-T_b=l/2 Q_3 \] \[ T_b-T_a1=d/k_1 Q_3 \] \[ T_a1-T_b1=l/k_2 Q_3 \] \[ T_b1-T_2=d/k_1 Q_3 \]

五个式子相加有： \[ T_1-T_2=(3d/k_1 +2l/k_2 )*Q_3 \] 设 \[ h=l/d,s=h k_1/k_2 \] 则得到 \[ Q_3=k_1 (T_1-T_2)/((3+2s)d) \]   对于双层玻璃，有如下示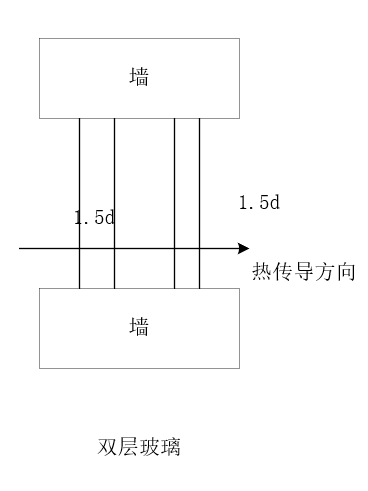意图：   我们可以做如下计算： \[ T_1-T_a=1.5d/k_1 Q_2 \] \[ T_a-T_b=l/k_2 Q_2 \] \[ T_b-T_2=1.5d/k_1 Q_2 \] 三式相加得到： \[ T_1-T_2=(3d/k_1 +l/k_2 ) Q_2 \] 设 \[ h=l/d,s=h k_1/k_2 \] 则得到 \[ Q_2=k_1 (T_1-T_2)/((3+s)d) \]   对于单层玻璃，有如下示意图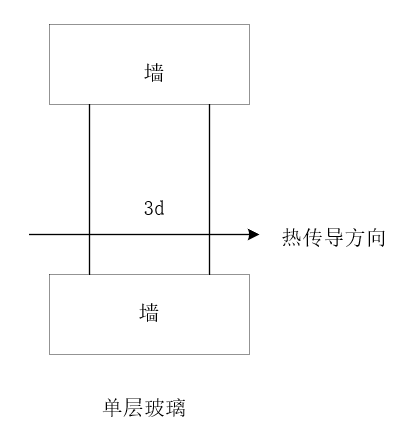：   可以做如下简单计算： \[ T_1-T_2=3d/k_1 Q_1 \] 得到 \[ Q_1=k_1 (T_1-T_2)/3d \]
六、模型求解

  要想对三种玻璃窗的保暖效果进行比较，只需要比较三个不同的热传导值，考虑两者之比：

\[ Q_3/Q_1 =3/(3+2s) \] \[ Q_2/Q_1 =3/(3+s) \] \[ Q_3/Q_2 =(3+s)/(3+2s) \] 显然 \[ Q_3<Q_1 \] \[ Q_2<Q_1 \] \[ Q_3<Q_2 \]   所以三层玻璃窗与两层玻璃窗减少的热量损失比小于同样多材料做的单层玻璃窗的热量损失。为了得到具体的结果，我们需要知道k_1和k_2的具体数据。从有关文献我们得到常用的窗户玻璃的热传导系数\(k_1=4*10^(-3)~8*10^(-3) J/(cm.s.℃)\)如果不流通，干燥空气的热传导系数\(k_2=2.5*10^(-4) J/(cm.s.℃)\)。 所以

\[ k_1/k_2 =16~32 \] 我们取最保守估计，即 \[ k_1/k_2 =16 \] 所以 \[ s=16h \] 则得到 \[ Q_3/Q_1 =3/(3+32s) \] \[ Q_2/Q_1 =3/(3+16s) \] \[ Q_3/Q_2 =(3+16s)/(3+32s) \] 其中 \[ h=l/d \] 利用matlab绘图，可视化表达，程序如下

1
2
3
4
5
6
7
8
9
10
11
12
clear
syms x
lims=[0 8];
y31=3/(3+32*x);
y21=3/(3+16*x);
y32=(3+16*x)/(3+32*x);
subplot(3,1,1)
ezplot(y31,lims)
subplot(3,1,2)
ezplot(y21,lims)
subplot(3,1,3)
ezplot(y32,lims)

运行程序可以得到如下图像 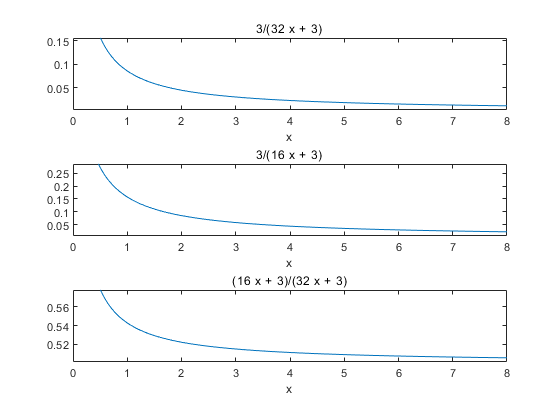我们发现：

  1. 上面三个图的比值反映了玻璃窗在减少热量损失的效果。它只与\(h=l/d\)有关，且由\(Q_3/Q_1\) 可知，当h由0增大时，\(Q_3/Q_1\) 比值快速下降，则表明三层玻璃窗的空隙越大，比单层玻璃窗的保暖效果越好，但是超过一定值之后，比值下降变缓慢，效果不太好。所以h不宜太大。
  2. 第二条曲线也是如此，在\(h>4\)时，\(Q_2/Q_1\) 比值开始变缓，第三条曲线反映的是\(Q_3/Q_2\) 随h的增大即玻璃之间的空隙越大，三层玻璃窗比两层玻璃窗的保暖效果就越好，不过\(h>4\)之后，效果不那么好，效果虽然强\(30\%~40\%\)，但是耗费的材料很多。而且比二层玻璃窗的保暖效果提高不了多少，所从经济与效果的层面上看，多数居民会选择二层玻璃而不是三层玻璃。
六、模型评价

模型优缺点：

  1. 本模型具有一定的应用价值，一般来说建筑规范要求h=l/d≈4，按照此模型双层玻璃窗比同样多材料做成的单层玻璃节约热量97%，效果十分不错，而三层玻璃效果没这么好。
  2. 由于模型假设的存在，上述分析都是在理想情况下的结论，所以三层玻璃的实际保暖效果与之相比会有一定的差距。
七、参考文献

[1]姜启源．数学模型[M]．北京：高等教育出版社，1993

[2]黄丽莉,侯君芳.三层玻璃窗与双层玻璃窗实用性比较[J].科技风,2010(4):237-237239

[3]刘敏.哈尔滨：节能新建筑须用三层玻璃外窗[J].墙材革新与建筑节能,2005(4):56-56